Download Question Paper of "data structures 2" , Question Paper of BCA (D) 2nd Semester, Subject Code : BCA-204, Paper ID 2037, Paper 3

Roll No......................

Total No. Of Questtions:13

Paper ID [ A0208]

BCA  (Sem.-2^nd)

B.Sc. IT(202)

MATH- I (Discrete)

Time : 03 Hrs.

Instruction to Candidates:

1.     Section – A is Compulsory

2.     Attempt any Nine questions from Section – B

SECTION – A

1.         

a.     Define inverse relation with example.

b.     Define into and onto functions.

c.      Prove AB= BA.

d.     Draw Venn diagram for the symmetrical difference of sets A and B.

e.      Define partition of a set with example.

f.       From conjunction of P and q for the following.

   P: Ram is healthy, Q : He has blue eyes.

g.     If p: It is cold, q: It is raining, write the simple verbal sentence which describe (i) P v q  ii) P v ~ q.

h.     Prove that proposition p v ~ p is tautology.

i.       Define logical equivalence.

j.       Define Biconditional statement .

k.     Define undirected graph with example.

l.       Edge of a graph that joins a node to itself is called ? And Edges joins node by more than one edge are called?

m.  Define  Null graph with example.

n.     Does there exist a 4- regular graph on 6-vertices, if so construct a graph.

o.     Prove V ( G₁  G₂) = V(G₁) V(G₂) with example .

Section –B

2.     Let R = {(1,2),(2,3),(3,1)} and A= {1,2,3}, Find Reflexive , symmetric. And transitive closure of R using composition of relation R.

3.     If  ƒ : A→B and g : B→C be functions , then prove

a.     If  ƒ and g are injections, then gof: A  → C is an injection.

b.     If ƒ and g are surjection then so is gof.

4.     Prove that A- (BC)=(A-B) (A-C)

5.     Show that set of real number in [0,-1] is uncountable set.

6.     A man has 7 relatives. 4 of them are ladies, and 3 are gentlemen , his wife has 7 relatives and 3 of them are ladies and 4 are gentlemen. In how many ways can they invite a dinner party of 3 ladies and 3 gentlemen so that there are 3 man’s relatives  and 3 of wife relatives.

7.     Using truth table show that ~ (p  q = (~p) v(~q).

8.     Consider the following :

P: it is cold day, q: the temperature is 50 c  writer the simple sentences meaning of the following:

(a)~p(b) p v q (c)~ (p v q)(d)~ p ~ q (e)~(~p v~q)

9.     Prove that following propositions are tautology.

a.     ~(p  q ) v q           b.  P →(p v q)

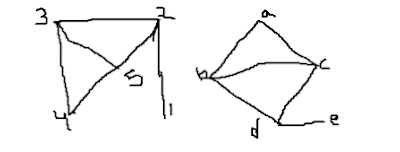
10.                         Show that two graphs shown in figure are isomorphic .

11.                        Prove a non – empty connected graph G is Eulerian if and only if all vertices are of even degree.

12.                        Define graph coloring and chromatic number with two examples of each.

13.                        Prove a simple graph G has a spanning tree if and only if G is connected.